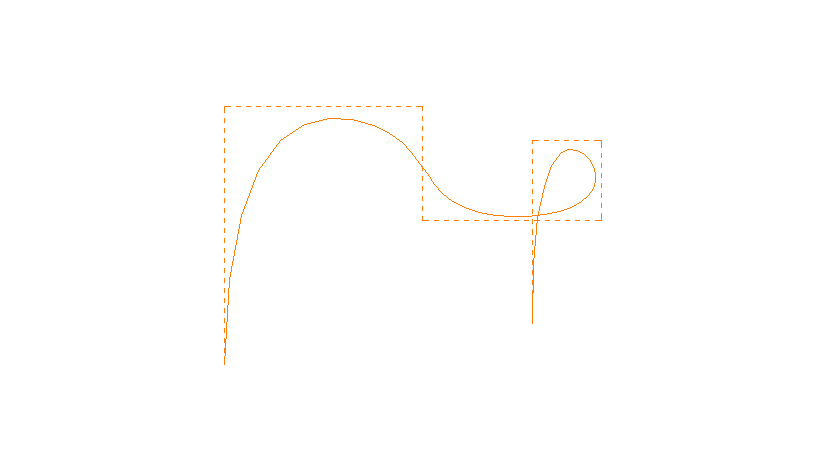> la 3D filaire
Cette approche est la plus simplifiée. Chaque arête est représentée et c'est pour cette raison que l'on parle de représentation "fil de fer". Cette technique ne permet pas l'élimination des lignes cachées, mais comporte toutes les bases de la conception 3D surfacique et volumique. On distingue :
1 > la ligne 3D
L'icône [Ligne] peut être utilisée en 2D comme en 3D. Tout dépend de l'entrée des coordonnées : un point 3D présente en plus des composantes en X et Y, une composante sur Z. Si la valeur Z est omise, elle adopte le zéro du SCU courant. Des lignes successives peuvent évoluer dans des plans de construction ayant des orientations différentes, mais chaque ligne est bien entendu toujours sur un même plan.
Exemple :
- Commande : _line
- Spécifiez le premier point : 0,0,2
- Spécifiez le point suivant ou [annUler] : @1,1,1
La syntaxe utilisée pour spécifier le premier point permet de le définir en coordonnées relatives au repère global. Le symbole @ permet de déclarer les coordonnées en repère local, dont l'orientation est, dans cet exemple, définie par rapport au premier point spécifié.
2 > la polyligne 2D
Assez étonnamment, Autocad fait toujours une différence entre les polylignes 2D et 3D... Les premières disposent de fonctions supplémentaires pour les modifieren tout cas sur ma vieille version CAD, peut-être se sont-ils améliorés sur les nouvelles... mais comme leur nom l'indique, elles ne peuvent être définies que dans un plan. Nous allons toutefois les étudier, car elles sont une entrée potentielle vers la courbe.
Exemple pour illustrer la polyligne 2D :
- Choisissez l'icône [polyligne] dans la barre d'outil [dessin].
- Dessiner un polygone quelconque par la saisie de points successifs comme sur l'illustration ci-contre.
Cette polyligne est éditable et vous pouvez la clore, l'ouvrir, la joindre à d'autres, modifier un des sommets et obtenir un lissage soit :
- en choisissant l'icône correspondante dans la barre d'outil [Modification II],
- en tapant au clavier [pedit] ou le raccourci clavier attribué à cette fonction dans le fichier acad.png.
Nous obtenons alors ceci :
- Commande: _pedit
- Sélectionnez la polyligne ou [Multiple]:
- Entrez une option : [Clore/Joindre/Epaiss/Modif-sommet/Lissage/sPline/Retrouver/TYpelignegén/annUler]
- Il suffit de taper la lettre de l'option proposée qui figure en Majuscule pour faire son choix. En tapant "l", vous obtenez un lissage par portions d'arc de cercle. Et si vous entrez "p", un lissage de type spline est proposé. Ce dernier dépend de la valeur de la variable système [splinetype] (5 correspond à un lissage par splines quadratiques ou "second ordre", vous pouvez ainsi dessiner une parabole à partir de 3 sommets ; 6 correspond à un lissage par splines cubiques ou "troisième ordre").
Un résultat identique et peut-être plus flexible selon les cas est obtenu en double-cliquant sur l'objet afin de faire apparaitre ses propriétés. Quelque soit le chemin choisi, la finesse de la représentation de votre courbe se règle par la variable système [splinesegs], fixée par défaut à 8 ce qui signifie que la courbe est discrétisée en 8 segments.
3 > la polyligne 3D
Contrairement à la polyligne 2D, la polyligne 3D accepte des variantes en Z. Dans le menu [dessin], choisissez [Polyligne 3D] ou ajouter manuellement l'icône dans la barre d'outil correspondante puisqu'elle n'apparait pas par défaut!
Les polylignes 3D sont éditables de la même façon que les 2D, avec moins de choix. Vous pouvez les clore, les ouvrir, modifier un des sommets et obtenir un lissage. Rappelons que le lissage par spline quadratique (second ordre) ne convient pas à une courbe 3D en raison de la discontinuité de la torsion, lui préférer un lissage au troisième ordre.
Dernière remarque : Les polylignes 2D ou 3D modifiées en spline par les modes d'édition proposés ci-dessus demeurent des objets Polylignes. Si vous souhaitez les convertir en véritables entités splines, allez dans le menu [Modifier/Objet/Spline].
4 > la spline
L'icône [spline] de la barre d'outil [dessin] est en fait une Nurbs (Non Uniform Rational B-Spline) cubique "par morceau" par défaut. La spline Nurbs donc, permet de préciser des points tridimensionnels. Elle peut être fermée ou ouverte. A la différence de la polyligne pour laquelle on définit les points de contrôle, la spline est définie par ses points de passage. Trois paramètres fournissent un contrôle de la courbe :
- Les points de contrôle (knots)
- Les poids des points de contrôle (weights)
- Le degré (local) de la courbe
Exemple pour illustrer la spline :
- entrez les points successifs par lesquels doivent passer la courbe
- et donnez la direction de la tangente des points extrémités. Il est possible de taper entrée pour ces deux dernières étapes. Dans ce cas, le logiciel calcul la spline au mieuxpour lui qui passe par les points à interpoler.
Cette spline est éditable et vous pouvez la clore, la poursuivre, déplacer les points de contrôle, en ajouter ou en supprimer, élever le degré ou changer la valeurs des poids ... :
- en choisissant l'icône correspondante dans la barre d'outil [Modification II],
- en tapant au clavier [editspline] ou le raccourci clavier attribué à cette fonction dans le fichier acad.png,
Remarquez que lorsqu'on édite une spline, les poignées ne sont plus les points interpolés mais les points de contrôle...
Nous obtenons alors ceci :
- Commande: _splinedit
- Sélectionnez une spline:
- Entrez une option [Lissée/Clore/Déplacer sommet/Affiner/Inverser/annUler]: a
- Entrez une option pour affiner [Ajouter point de contrôle/Elever ordre/Poids/Quitter] : p
- La spline n'est pas rationnelle. Rationalisation de celle-ci.
- Entrez un nouveau point (courant = 1.000) ou [suivaNt/Précédent/sélecTionnez point/Quitter] : n
- Entrez un nouveau point (courant = 1.000) ou [suivaNt/Précédent/sélecTionnez point/Quitter] : n
- Entrez un nouveau point (courant = 1.000) ou [suivaNt/Précédent/sélecTionnez point/Quitter] : n
- Entrez un nouveau point (courant = 1.000) ou [suivaNt/Précédent/sélecTionnez point/Quitter] : 10
Il suffit de taper la lettre de l'option proposée qui figure en Majuscule pour faire son choix. Pour l'exemple, nous avons choisi d'illustrer l'influence du poids d'un point de contrôle sur la forme de la courbe. Initialement, tous les poids sont fixés égaux à 1 (donc initialement, nous avons bien une spline), c'est pour cela que la boite de dialogue nous parle de rationalisation. Le fait de rentrer une valeur positive et différente de 1 transforme véritablement la courbe en Nurbs.
Nous vous laissons le loisir de découvrir les autres options.